1. Pacing: Determine the length of your stride by walking at your normal rate over a measured distance. Divide the distance by the number of steps, giving you the average distance per step. Knowing this, you can pace off horizontal distances.I walk at a rate of _____ paces per ________....or....My pace = _______
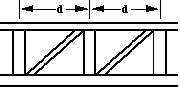
2. Ride Structure: Distance estimates can be made by noting regularities in the structure of the ride. For example, tracks may have regularly spaced cross-members as shown in figure A. The distance d can be estimated, and by counting the number of cross members, distances along the track can be determined. This can be used for both vertical and horizontal distances.
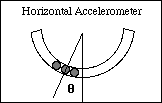
3. Triangulation: For measuring height by triangulation, a horizontal accelerometer can be used. Suppose the height h of a ride must be determined. First the distance L is estimated by pacing it off (or some other suitable method). Sight along the accelerometer to the top of the ride and read the angle q . Add in the height of your eye to get the total height.
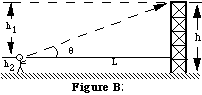 tan q = h1 / L , h1 = L tan q h2 = height of eye from ground
tan q = h1 / L , h1 = L tan q h2 = height of eye from groundh = total height of ride = h1 + h2
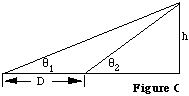
4. A similar triangulation can be carried out where you cannot measure the distance to the base of the ride. Use the law of sines as illustrated in Figure C to the right:
Knowing q1, q2 and D, the height h can be calculated using the expression:
h = ( D sin q1 sin q2 ) / sin (q2 - q1)