Accelerometers work by detecting forces. We look at the force acting on a small mass, divide it by the object's mass, and calculate the force per unit mass. The ratio, which ends up in units of N/kg, is the same regardless of the amount of mass. These units are conveniently equivalent to acceleration units (m/s2), and thus the sensor can be used to make direct measurements of acceleration for objects that are moving linearly.At the amusement park the predominant use of accelerometers is to indicate sizes and directions of forces experienced by riders. The origins of those forces, combinations of gravity and the actions of the rides, leads to forces that vary in size and direction throughout a ride experience. The electronic accelerometer is well suited for recording these forces. Traditional hand-carried accelerometers work in the same manner.
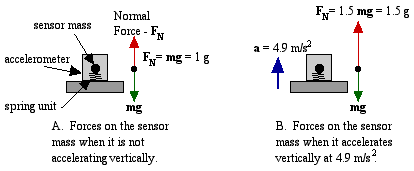
Visualize the accelerometer having a small mass unit that is held in place with a spring element. This is shown in the diagram below.

When the sensor is not accelerating in a vertical direction (A), the spring element must exert a force upward equal to the weight of the mass, mg. A voltage is sent to the interface that we interpret as either 9.8 N/kg or 1 g. But if the sensor is accelerated upwards at 4.9 m/s2 (B), half the normal free-fall acceleration of gravity, the spring element must exert a larger force to accelerate the mass unit. The new force is 1.5 mg, or we could say that it is 14.7 N/kg or 1.5 g's. In this way, the sensor is constantly monitoring the upward force exerted on the mass unit, and by extension, the upward force exerted on us.If we have the accelerometer oriented horizontally, the situation is diagrammed as shown below. If there is no horizontal acceleration (C), the spring unit does not have to exert a force on the mass. The voltage sent to the interface would be interpreted as 0 N/kg or 0 g's. However, if the sensor is accelerated at 4.9 m/s2 (D), the spring unit must exert a force equal to 0.5 mg, and the voltage is interpreted as 4.9 N/kg or 0.5 g.

It is important to note that whether the accelerometer is oriented vertically or horizontally, the force we are talking about is normal to the support. Although it's a mouthful, we label the readings "Normal Force Per Unit Mass", although we may shortcut this to "force/mass", "F/m" or simply "force".Units: Accelerometers are usually calibrated in units of m/s2. This is the same as N/kg and we infer that we are measuring normal force per unit mass even though the units seem to say acceleration. 9.8 m/s2 is the same as 9.8 N/kg, which could also be interpreted as 1 g, while 19.6 m/s2 or 19.6 N/kg would be 2 g's, etc. We recommend converting the units to N/kg or g's to emphasize the nature of the readings.
Axes: In practice, we analyze different axes separately. We discuss the forces in the forward/reverse (longitudinal), side-to-side (lateral), or up and down (vertical) directions. Breaking the forces up into the three major axes relative to our bodies and our motion helps us to explain the different forces we are experiencing and what led to those forces.
If we are standing still or moving along a level track at a constant speed, there is one unit of force from gravity pulling us downward. The ground or seat exerts an opposing 1-g force upward on us to counteract this downward force. We feel this force constantly in our daily lives, and almost forget that it's there. Elevators that are rising or descending at a constant speed also exert a constant 1-g upward force on us.
The accelerometer measures the combined effects of both gravity and any actions of the ride we are on at the time. On a typical roller coaster, there is a dip following the lift hill. As the riders pass through the bottom of the dip, they feel a very large upward force from the seat. This force is partly due to counteracting gravity and partly due to changing our motion into the curved path, which requires a net force towards the center, which is up at that point. So the force here is typically several times that of normal gravity.
When the riders go over the top of a bump with some speed, they feel lighter than normal, almost as if they were lifted out of the seat. Again this is due to the reaction to gravity and the effect of the ride's motion. The center of the curve is below the riders so part of the gravitational force is used to pull them down towards the center, leaving less of their weight that must be supported by the seat. The force recorded here will be less than 1 g.
If the riders go over a bump with sufficient speed, they may feel the car moving out from beneath them, and they are pulled down by the restraint system. This is called "negative g's". The car is held on the track by wheels that ride below the track, while the shoulder harness pulls the rider down.
When riders go through a vertical loop, their force reading varies throughout the loop for several reasons. For one, the angle relative to gravity changes throughout the loop. The speed also changes due to climbing up the side of the loop then rolling down the other side. Finally, the degree of curvature in the loop changes. To understand the force readings throughout the loop one must understand how all of these factors are playing out. For example, on the side of the loop, whether rising or descending (A or C in the diagram below), gravity acts along the longitudinal axis of the rider but not along the vertical axis. At the top of the loop (B), gravity acts to help hold the rider in the circular path, acting in a centripetal manner. The total force needed to go in the circular path, mv2/R, is partially supplied by gravity so the seat force towards the center of curvature at that moment is [(mv2/R) - mg]. If designers have calculated correctly, the seat will supply a force on the riders, holding them in their seat throughout the ride.
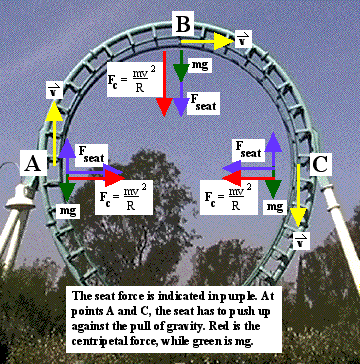
As this discussion shows, the combination of gravity and the ride forces is complex. This is one of the fascinating aspects of amusement parks - trying to unravel the complexity presented by the twists and turns of the rides.
March 2004