 CENTRIFUGE
CENTRIFUGE CENTRIFUGE
CENTRIFUGE
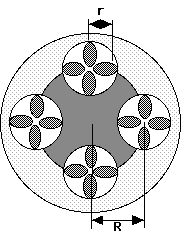
DATA:Radius of primary axis (R) (measured from center of ride to center of car cluster): ________Radius of secondary axis (r) (measured from center of car cluster to center of car): ________
Indicate on diagram the directions of rotation (as seen from above)
Period of rotation of the whole platform: _______
Period of rotation of car cluster: ________
Maximum lateral acceleration (aL): __________ g's (measured on the ride at full speed)
Minimum lateral acceleration (aL): __________ g's (on ride at full speed)
Measure the angle the whole ride makes to the horizontal: ________
In the problems that follow, ignore the fact that the entire ride is set at an angle to the horizontal. Consider the ride as if it were running in a horizontal manner. Consider a passenger who is seated nearer the outside of the ride rather than closer to the inside.
PROBLEMS (to be answered on back or separate page)
 CENTRIFUGE
CENTRIFUGE
Math-oriented
Radius of primary axis (R) (measured from center of ride to center of car cluster): ________Radius of secondary axis (r) (measured from center of car cluster to center of car): ________
Indicate on diagram the directions of rotation (as seen from above)
Period of rotation of the whole platform: _______
Period of rotation of car cluster: ________
In the problems that follow, ignore the fact that the entire ride is set at an angle to the horizontal. Consider the ride as if it were running in a horizontal manner. Consider a passenger who is seated nearer the outside of the ride rather than closer to the inside.
PROBLEMS (to be answered on back or separate page)
 CENTRIFUGE
CENTRIFUGE
Math-oriented
DATA:
Radius of primary axis (R) (measured from center of ride to center of car cluster): ________Radius of secondary axis (r) (measured from center of car cluster to center of car): ________
Indicate on diagram the directions of rotation (as seen from above)
Period of rotation of the whole platform: _______
Period of rotation of car cluster: ________
Maximum lateral acceleration (aL): __________ g's (measured on the ride at full speed)
Minimum lateral acceleration (aL): __________ g's (on ride at full speed)
In the problems that follow, ignore the fact that the entire ride is set at an angle to the horizontal. Consider the ride as if it were running in a horizontal manner. Consider a passenger who is seated nearer the outside of the ride rather than closer to the inside.
PROBLEMS (to be answered on back or separate page)