Depth of Field
Pinhole Camera
f-Stops
Depth of Field
A camera is replete with examples of physics, ranging from levers and other simple machines to the advanced electronics that controls the lens and shutter in most modern cameras. The purpose of this part of the web site, though, will be to deal with one aspect of cameras, namely the phenomenon called "depth of field."
It seems that when we adjust the aperture down to a smaller opening, the depth of field increases, meaning that objects from a wider range of distances will appear focused.
We'll use ray diagrams to investigate this idea, and will try to show how stopping a lens down (making its aperture smaller) will lead directly to depth of field. In the diagrams which follow, there is a lens and two objects. The nearer object is solid while the further object is shaded. Notice where each forms its image in our example, and then keep following along.

This is the basic setup showing the lens, the two objects, the axis of the lens and the two focal points, one on each side.
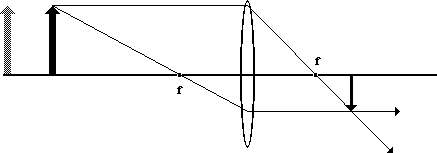
We form the image of the solid object first. This is just a basic ray diagram.
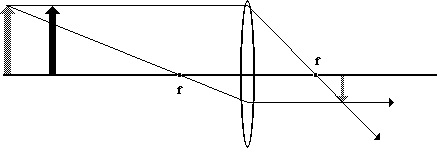
Then we form the image of the gray object. The two images don't fall the same distance from the lens. This is shown in this diagram:

For discussion sake, we make the two images the same size but retain their respective distances from the lens. Now place a piece of film where the solid image is located in order to obtain a sharp image of it.

Follow light rays as they go from the shaded object and hit all over the lens. The result is a "zone of confusion" in the plane of the film. In other words, the gray image is blurry.

If we introduce an aperture which reduces the size of the lens opening, notice how it also cuts down on the size of the zone of confusion. Making the opening smaller reduces the amount of spreading out the image does after it has become a sharp image.
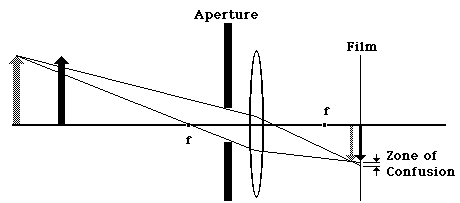
And cutting down the aperture opening further reduces the zone of confusion even more. At this point the two images, dark and gray, are almost equally sharp.
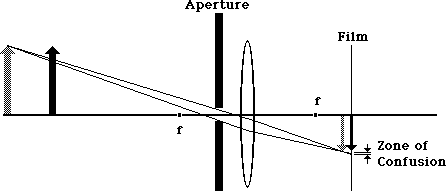
The phenomenon of Depth of Field, thus, is due to a geometric aspect. By reducing the size of the aperture, the angle that light passes through the lens and then through the image is reduced. The degree to which the image is fuzzy has gone down.
In point of fact, only objects at one particular distance are clearly in focus. But if there is a small angle involved, objects at other distances will appear to also be clearly focused.
PINHOLE CAMERA
A Pinhole Camera consists of a small aperture that light passes through, a dark enclosure, and a piece of film. As shown in the diagram below, an object placed in front of a Pinhole Camera forms a clear image on the film without the need for a lens.
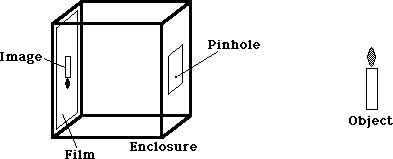
Because the aperture is so small, from each point on the object, only one ray of light may pass through and then move on to the film. Thus there is a one-to-one correspondence between points on the film and points on the object.
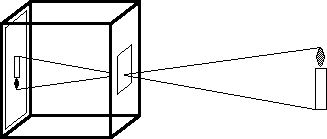
If we look at the possibility of changing the distance from the pinhole to the film, we see that we can affect the size of the image of a given object. Compare the size of the images below at three different image distances.

Now, if we only consider energy, the energy concentration in the smaller image is higher, and thus a shorter time is needed to expose the film. The concentration in the larger image is less, so a longer time is needed. Photographers in the past developed a good understanding of this relationship.
If by accident more than one pinhole is opened, multiple images are formed, one from each pinhole. Such an occurrence is diagrammed below.

A very interesting phenomenon occurs, however, if a lens of the correct focal length is inserted between the pinholes and the film. The multiple images become a single image. This is dramatically shown in the PSSC film "Introduction to Optics." The demonstration is shown below schematically.

The explanation for this phenomenon will await an updated version of this stack. The author believes that a correct explanation, though, will demonstrate good understanding of not only pinhole cameras, but of image formation in general.
f-STOPS
The question we confront at this point is the unusual pattern of aperture opening numbers. On an adjustable camera, the f-stops come in a sequence like the following:
Why does this particular sequence exist, and what does it mean? Is it related to physics?
In understanding this puzzle, we first note that the aperture is the opening through which light enters the camera to expose the film. The larger the opening, the more light energy per second enters. Therefore, we would imagine that a larger number would indicate a larger aperture.
In fact, a larger f-stop number indicates a smaller aperture. f/22 is a much smaller opening than f/2.
One clue to the puzzle comes from the notation, f/22. With a larger number in the denominator, a fraction has a smaller value. Therefore there must be an inverse relationship of some sort here.
Another interesting clue comes from the relative sizes. From 1.4 to 2.0, from 2.0 to 2.8, from 8 to 11 the size of the number increases approximately 1.4 times each step. This is almost exactly the square root of 2. From 2.0 to 4.0 requires 2 steps to double, while from 4.0 to 8.0 also requires 2 steps.
Therefore we can home in on an answer. The f-stop is a reciprocal number, indicating 1 divided by some factor. As the f-stop increases one "step", the denominator increases by the square root of 2, or the fraction reduces by 1 over the square root of 2.
This number refers to the diameter or the radius of the aperture. If the radius is reduced by the square root of 2, the area is reduced by a factor of 2. But this is indicated by increasing the f-stop by 1.4 times!
Consult the chart below to see the relative change in light energy admitted to the camera, assuming the camera is opened for equal amounts of time.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The application of physics here involves the interplay between aperture opening and shutter speed. Both are set up roughly into factors of 2. Shutter speeds go 1/30, 1/60, 1/125, 1/250, etc.
By increasing the shutter speed say from 1/60 to 1/125, one decreases the light by a factor of 2. To compensate, he/she opens the shutter up by changing the f-stop one setting, say from f/8 to f/5.6. Knowing these factors of 2 can be of great assistance in estimating exposure settings for the serious photographer.