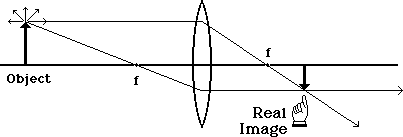
In the diagram above, two principle rays are used to locate the real image that is to the right of the lens and inverted.
TOWARDS AN EQUATION:

In this diagram, several lines are given symbols which are used to designate their lengths. The chart below defines each. Typically these would be measured in centimeters or possibly millimeters. In astronomical systems, meters might be used.
|
|
|
|
|
Size (height) of object. (o represents object) |
|
|
Distance from lens to the object |
|
|
focal length (lens to focal point) |
|
|
Distance from first focal point to object |
|
|
Size (height) of image (i represents image) |
|
|
Distance from lens to image |
|
|
Distance from second focal point to image |
APPROXIMATION:
We consider the thickness of the lens to be small compared to the distances involved. We think for simplification that the light rays do all of their bending in the center of the lens rather than the two sides. This gives us the ability to do some basic geometry as shown in the diagram which follows.

The lightly shaded triangles on the left form similar triangles because they share vertical angles. (We assume the object is perpendicular to the axis as is the lens.) Likewise we get similar triangles on the right, the more darkly shaded ones.
Because both equations contain the term Ho/Hi, we can set the remaining terms equal to each other and we get the equation below.
If we cross-multiply the right hand terms and expand the binomials, we get the following:
We now subtract f2 from both sides and then move the terms with f to the left-hand side:
Now factor out the f and move the binomial to the right-hand side:
Here we invoke a mathematical trick, even though the equation looks okay (and it is). Take the reciprocal of the entire equation, and then expand the right-hand side:
There it is! An equation that predicts the image location based on the object distance and the focal length. Any number of problems can be derived from this equation, and it will be seen to be applicable for four different optical devices! (Five if you stretch things.)
We now go on to find another equation, based on a third light ray that also works with the final image.

We see that there will be similar triangles if we assume both the object and image are perpendicular to the axis, and if we assume the lens is thin and the light doesn't deviate from a straight line very far. This gives us the following equation:
This equation gives the ratio of image size to object size in terms of image distance and object distance. This ratio is also called the magnification, m. It is easy to see that if the real image is formed further from the lens than the object is placed, the image will also be larger.
What are some predictions from this equation?
1. If the object distance is very large, the image distance will be f, the focal length. ie, the image will be formed one focal length away from the lens.
Substitute a large value for Do in the first equation. Make it infinity (mathematicians don't like that concept, so they often call it GBN, Great Big Number). Now 1/infinity or 1/GBN is zero or almost zero.
2. If the object distance is f, the image distance will be undefined, or infinite. In practice, the lens will form a set of parallel light rays that will neither converge or diverge, so no image is ever formed.
3. The object and image distances will be equal at the point where they are both 2f.
SIGNS:
For lenses, we develop a sense of signs in our mathematics. It comes from the direction that light travels through the lens. In the diagram which follows, note that the positive sense of things occurs when light starts on one side and converges on the other.
|
Object distance is positive |
Object distance is negative (very rare) |
|
Image distance is negative |
Image distance is positive |
|
Focal point is negative |
Focal point is positive |