PURPOSE:
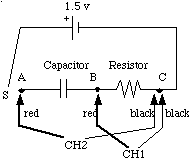
CIRCUIT:

MATERIALS:
PROCEDURE:
2. Connect the CBL voltage probes to the Capacitor Charge/Discharge
Apparatus as shown. Use 50 µF for the capacitor and 10 K_
for the resistor. Make sure the switch is in "DIS" or
discharge position. To make sure the capacitor is fully discharged,
touch a piece of wire between points A and B. Remove
this wire for the following steps.
3. Launch the program "CAPACITO". Enter the resistance
in ohms and the capacitance in micro-farads (µF) when asked.
Press <ENTER> to begin collecting data. When the display
on the CBL indicates "SAMPLING", flip the switch to
"CHG".
4. After a few seconds, you will be presented with a menu.
Choose "CAPACITOR VOLTS" to look at the voltage across
the capacitor; choose "CURRENT-TIME" to look at the
current flowing in the circuit, or choose "V-T AND I-T"
to look at both graphs. After examining a graph, press <ENTER>
to return to the menu.
> > > Sketch and describe the shapes of both graphs
for capacitor charging. Describe the relationship between the
two graphs and what is happening in the circuit.
5. With the capacitor fully charged, choose "NEW DATA
RUN". When you press <ENTER> to begin collecting data,
and the CBL displays "SAMPLING", flip the switch to
"DIS". Follow the process in step (4) and answer the
same questions above.
6. Go to the ANALYSIS section.
7. Try other resistor-capacitor combinations as time permits, obtain the new components from the instructor.
ANALYSIS:
2. Press <STAT> then use the right arrow to select "CALC".
Now use the down arrow go move to "A: ExpReg" and press
<ENTER>. At the cursor position, press this sequence: <2nd>
<L1> <,> <2nd> <L2>
and then <ENTER>. The calculator will now evaluate the data
for an equation of the form y = a * b^x. Enter the values
for a and b in the data table.
3. The value "b" is equivalent to e-k.
If e-k = b, then k =
-ln b. Determine the value for k and enter it in your
data table.
4. Write out the exponential equation that describes the voltage
drop in your experiment:
y = a e-kt =
5. Plot the equation above on top of your lab data to check the
accuracy of this equation in predicting the voltages encountered
while discharging a capacitor.
6. Take the inverse of the product of the resistance and the capacitance.
Check the units of this product. and compare the final value to
the value of k in your equation in step 4.
What is the percentage difference between your values in steps
4 and 6? To which factor should any difference be primarily attributed,
the capacitor value or the resistor value? Why?
DATA:
Exponential Regression: a _______________
Exponential Regression: b _______________
Exponent: (k) _______________
Resistance Capacitance: (RC) _______________
Inverse RC: (RC)-1 _______________
Percentage Differnce: _______________
Note: The connections for the PC boards are shown here:
