LAB INVESTIGATION TWO
GRAPHING FREE FALL
PURPOSE:
The purpose of this investigation is to determine the equation which describes the displacement of an object in free fall.
EQUIPMENT:
The equipment for this experiment includes the following:
- Digital Timer
- Impact Detector Board
- Ball Release Switch
- Meter Stick
- C-clamp
- Steel Ball Bearing
SET UP:
Carry out the following instructions to set up the experiment:
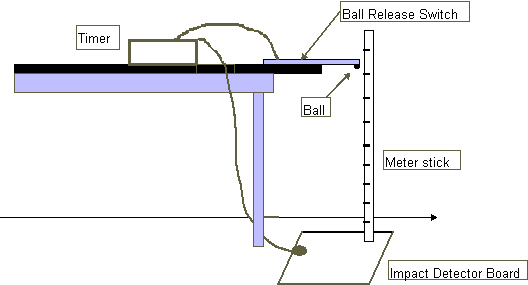
- Use the C-clamp to attach the Ball Release Switch to the lab table as shown in Figure 1. The release point should extend at least ten centimeters past the edge of the table.
- Place the Impact Detector Board on the floor directly under the release point. Make sure the ball will not strike the microphone on the Impact Detector Board.
- Connect the Ball Release Switch to terminal 1 and the microphone on the Impact Detector Board to terminal 2 on the Digital Timer.
- Hold down the green mode button until both of its lights are out, indicating the binary code "00" which stands for "STOP ON B".
- Push repeatedly the blue button which moves the decimal place of the time reading until the decimal point light shows the place where the most precise readings can be made for times up to 1.000 second. This should produce the following timer settings:
- Timer Settings>:
Blue Decimal: XXXX. ms
White SWITCHES: 00 NORMAL
Green MODE: 00 STOP ON B
Figure 1 - Diagram of Equipment Set Up
PROCEDURE:
Carry out the following steps to gather data for this experiment:
- With the Impact Detector Board on the floor measure the Height from the Impact Detector Board to the bottom of the ball. Record this Height in Table 1.
- Release the ball and record the time of flight. Repeat four more times and record the times in Table 1.
- Raise the Impact Detector Board by putting three physics books underneath it. Repeat Steps 1 & 2.
- Repeat Step 3 until you have carried out 8 to 10 trials.
INDIVIDUAL DATA AND RESULTS:
TABLE 1 - DATA and RESULTS
| TRIAL |
HEIGHT |
TIME 1 |
TIME 2 |
TIME 3 |
TIME 4 |
TIME 5 |
MEDIAN TIME |
TIME2 |
|
y |
t1 |
t2 |
t3 |
t4 |
t5 |
tmedian |
t2 |
|
m |
sec |
sec |
sec |
sec |
sec |
sec |
sec2 |
| 1 |
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
| 7 |
|
|
|
|
|
|
|
|
| 8 |
|
|
|
|
|
|
|
|
| 9 |
|
|
|
|
|
|
|
|
| 10 |
|
|
|
|
|
|
|
|
ANALYSIS OF INDIVIDUAL RESULTS:
- For each trial determine the median value of the time. Record this in Table 1.
- Graph Height vs. Median Time.
- Describe this graph and write an equation that you think would fit the graph.
- Graph Height vs. the square of the Median Time.
- Draw a best fit median line for the graph in Step 4.
- Calculate the slope for your best fit line.
- How does the slope obtained in Step 5 relate to the equation describing your first curve.
- What is the value of twice your slope value?
CLASS RESULTS:
Record twice the slope values of all students in the class in Table 2:
TABLE 2 - RESULTS FOR THE CLASS>
| STUDENT | 2*SLOPE VALUE |
| m/s2 |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
ANALYSIS OF CLASS RESULTS:
Carry out an Exploratory Data Analysis of the class results.
- Construct a Line Plot of twice the slope values for the class.
- Using the results of the Line Plot, construct a Stem & Leaf Plot of these values.
- Determine the minimum value,1st quartile, median value, 3rd quartile, and maximum value for the results.
- Construct a box plot using the values obtained in Step 3.
- Determine the relative difference between your value of twice the slope and the median value obtained from the set of class data.
CONCLUSIONS:
Discuss the results that were obtained in this experiment. Use the following questions to guide you in this write up:
- What was the shape of the Height vs. Time graph for a freely falling object? What is its equation?
- How is the slope obtained from the graph of Height vs. Time Squared related to the coefficient in the Height vs. Time equation?
- How does your value of twice the slope compare to the median value obtained from the class results?
- What does the box plot tell you about the class results for this experiment?
- Where is your value in the box plot?
- What does twice the slope value represent?
- Would the result obtained for this experiment be different, if the initial height was different?
- How could you use the equation obtained for this experiment to verify your answer to the previous question?
Written by John Thompsen, July 1997