

The data below was gathered while observing the manner in which light intensity dropped off as the student moved away from a light source. Use one or more of the four methods of analyzing the data to see if you can discover the mathematical relationship. If you think you have the form of the proportion, then go ahead by clicking the method you used to do the analysis. |
|||||||||||||||
|
|
|||||||||||||||
|
|||||||||||||||
|
|
|||||||||||||||
|
If you have determined the relationship, click on your method of analysis to verify your technique. You can also check out other methods of arriving at the same conclusion. |
|||||||||||||||
|
|||||||||||||||
 |
Comparing two of the values on the left, we find that doubling the distance yields a decrease in intensity by a factor of 1/4. |
||||||||
 |
Comparing a different two values on the left, we find that increasing the distance five times yields a decrease in intensity by a factor of 1/25. |
||||||||
 |
Finally, comparing a different two values on the left, we find that decreasing the distance to 1/2 yields an increase in intensity by a factor of 4 times |
||||||||
|
Now, the table to the left shows us a summary of the changes we've talked about in the past three tables. We notice two things about the relative changes. First, when the Control variable increases, the Dependent variable decreases. |
||||||||
|
As a result, we have a type of Inverse Proportion. Second, the factors for change in the Dependent variable are larger than those in the Control. They look to be, in fact, the Square of the Control factors. |
||||||||
|
By examining the changes carefully, we assure ourselves that this is correct, and wind up with the conclusion that the relationship is both inverse and square, leading to what we call an "Inverse Square" proportion. |
||||||||
 |
As shown on the left, an Inverse Square proportion can be written in several ways. Satisfy yourself that you can write and understand each one before going on. |
|
 |
The graph of Intensity vs Distance is shown here. To check for characteristic curve, we compare it to the four curves that were generated previously. The simplest one is a straight line graph, the characteristic for a direct proportion. With little effort, we convince ourselves that the data does not give a straight line! |
 |
A second characteristic curve that doesn't fit our graph is the upward curve plotted for a square proportion. Our graph definitely is different. |
 |
A third characteristic curve that doesn't fit our graph is the curve plotted for a square root proportion. Our graph is different again. |

|
Finally we come to the Inverse Proportion graph, and we see that there are definitely similarities to our unknown data's graph. We would be pleased to simply call it an inverse proportion, but may wish to reserve judgement until further tests are made. At this point we move to the Straight Line Graph section and test the data further. |
|
 |
There is definitely the indication of an inverse relationship in the data from this experiment. If it is a strictly inverse proportion, then plotting the intensity vs the reciprocal of distance will yield a straight line graph. That is what we'll do on the next page. |
 |
Plotting 1/Distance along the horizontal axis does not straighten out the graph. Rather, it now resembles a square proportion, curving upwards. Taking a cue from this upward curve, we might try squaring the 1/Distance values and re-plotting the graph. This is done on the next page. |
 |
By plotting the reciprocals of the distances squared versus the intensities, we now have a straight line graph. This is a solid indication of the type of proportion that is at work in this lab. From the graph we can immediately write: |
 |
The mathematical proportion derived from the straight line states that the intensity (I) is directly proportional to the square of the reciprocals of the distance (1/d2). A proportion of this type is called an "Inverse Square" proportion. |
 |
As shown on the left, an Inverse Square proportion can be written in several ways. Satisfy yourself that you can write and understand each one before going on. |
|
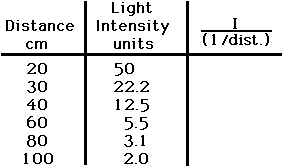 |
Since an increase in distance yields a decrease in light intensity, we construct a table with the ratio of light intensity to 1/distance. |
 |
This operation does not yield a constant ratio, therefore we cannot simply say that this is an inverse proportion. At this point we try several combinations, to get one that hopefully works. |
 |
The one combination that does work for us is when we square the 1/distance values and divide them into the intensities. Thus we see that there is both a square and an inverse component. |
 |
This unique combination of variables is called an "Inverse Square" proportion, and has several very important applications in our physical world. |
 |
As shown on the left, an Inverse Square proportion can be written in several ways. Satisfy yourself that you can write and understand each one before going on. |
|
|
In this example of an "unknown" proportion, we found that the dependent variable was proportional to the inverse square of the control variable. This proportion can be simply written: In our case, the dependent variable was light intensity, I, and the control variable was distance, d. Re-writing the proportion using specific symbols gives us: |
What does this proportion tell us about how light intensity changes as the distance from the source changes?1. If we double the distance, the intensity drops to 1/4 its former value. |
Where else does such a relationship show up?1. In terms of radioactivity, the decrease in exposure drops as the inverse square of the distance. |
In short, then, this new "unknown" relationship which we can show to be "Inverse Square" shows up in at least four major places in the world in which we find ourselves. |
Hopefully you were able to follow these arguments, at least, and at best were able to develop them yourselves. |
|
Updated August 2001