
Figure 1
The primary objective of this experiment is to determine the relationship between the pressure and volume of a confined gas. The gas we use will be air, and it will be confined in a syringe connected to a Gas Pressure Sensor (see Figure 1). When the volume of the syringe is changed by moving the piston, a change occurs in the pressure exerted by the confined gas. This pressure change will be monitored using the Gas Pressure Sensor. It is assumed that temperature will be constant throughout the experiment. Pressure and volume data pairs will be collected during this experiment and then analyzed. From the data and graph, you should be able to determine what kind of mathematical relationship exists between the pressure and volume of the confined gas. Historically, this relationship was first established by Robert Boyle in 1662 and has since been known as Boyle’s law.OBJECTIVES
In this experiment, you will
- Use a Gas Pressure Sensor and a gas syringe to measure the pressure of an air sample at several different volumes.
- Determine the relationship between pressure and volume of the gas.
- Describe the relationship between gas pressure and volume in a mathematical equation.
- Use the results to predict the pressure at other volumes.

Figure 1
MATERIALScomputer, Vernier computer interface, Logger Pro, Vernier Gas Pressure Sensor, 20-mL gas syringePROCEDURE
- Prepare the Gas Pressure Sensor and an air sample for data collection.
- Plug the Gas Pressure Sensor into Channel 1 of the computer interface.
- With the 20 mL syringe disconnected from the Gas Pressure Sensor, move the piston of the syringe until the front edge of the inside black ring (indicated by the arrow in Figure 2) is positioned at the 10.0 mL mark.
- Attach the 20 mL syringe to the valve of the Gas Pressure Sensor.
- Prepare the computer for data collection by opening the file "06 Boyle’s Law" from the Chemistry with Vernier folder of Logger Pro.
- It is best for one person to take care of the gas syringe and for another to operate the computer. Click
to begin data collection.
- Move the piston to position the front edge of the inside black ring (see Figure 1) at the 4.0-mL line on the syringe. Hold the piston firmly in this position until the pressure value stabilizes.
- When the pressure reading has stabilized, click
. Type the gas volume in the window that appears. Press ENTER to keep this data pair. Note: You can choose to redo a point by pressing the ESC key (after clicking
but before entering a value).
- Move the piston to the 6.0-mL line. When the pressure reading has stabilized, click
and type in the volume.
- Continue this procedure for syringe volumes of 8.0, 10.0, 12.0, 14.0, 16.0, 18.0 and 20.0 mL.
- Click
when you have finished collecting data.
- Proceed to the next steps, keeping your data on the computer screen.
PROCESSING THE DATA
General
- Click the Examine button. Move the vertical cursor until it is over the 4.0-mL data point. What is the pressure at this volume? Now move to the 8.0-mL volume and note the pressure here. What does your data show happens to the pressure when the volume is doubled? Include your pressure values in your answer.
- Move to 12.0-mL volume and note the pressure. What happens when the volume is tripled? Include your pressure values in your answer.
- Using the same technique as in Step 1, what does your data show happens to the pressure if the volume is doubled from 10.0 mL to 20.0 mL? Include the pressure values in your answer.
- Using the same technique as in Step 1, what does your data show happens to the pressure if the volume is halved from 16.0 mL to 8.0 mL? Show the pressure values in your answer.
- Using the same technique as in Step 1, what does your data show happens to the pressure if the volume is tripled from 6.0 mL to 18.0 mL? Show the pressure values in your answer.
- From your answers to the first four questions and the shape of the curve in the plot of pressure vs. volume, do you think the relationship between the pressure and volume of a confined gas is direct or inverse? Explain your answer.
- Based on your data, what would you expect the pressure to be if the volume of the syringe was increased to 40.0 mL? Explain or show work to support your answer.
- Based on your data, what would you expect the pressure to be if the volume of the syringe was decreased to 2.0 mL? Explain or show work to support your answer.
Curve Fit
- Click on the Examine button to put away the vertical cursor. Based on your examination of the data, you have decided on the type of mathematical relationship you think exists between these two choices, direct or inverse. To see if you made the right choice:
- Click the Curve Fit button,
.
- Choose Variable Power (y = Ax^n) from the list at the lower left. Enter the power value, n, in the Power edit box that represents the relationship shown in the graph (e.g., type "1" if direct, "-1" if inverse). Click
.
- A best-fit curve will be displayed on the graph. If you made the correct choice, the curve should match up well with the points. If the curve does not match up well, try a different exponent and click
again. When the curve has a good fit with the data points, then click
.
- You should have fairly good agreement between your mathematical model for this relationship, but it may also resemble the following graph:
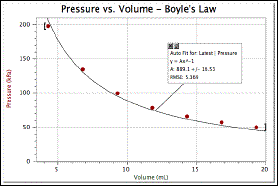
Discrepancy
- Close examination of the graph indicates the model curve fit line starts above the data points and ends up below the data points in a very regular manner. Although the fit is fairly good, it is not conclusive proof of the relationship. This pattern is indicative that something might be working in the experiment that has not been previously accounted for.
- Let’s examine our equipment a bit more closely. If you take the syringe off of the Gas Pressure Sensor, and press the plunger down so the volume reads "0", note the small but non-zero amount of air that still remains in the end of the syringe. A similar air pocket likely exists inside the Gas Pressure Sensor, too. So the volume readings we have been recording, the values on the syringe, are not the true volumes of air.
- One method of dealing with the discrepancy is to add a figure known to be an approximate value of the extra air volume to each of the recorded volumes. The re-drawn graph will then produce a better curve fit than the one you just had.
- Under Data on the menu bar, choose New Calculated Column. Use a name like "Real Volume" and a short name like Vr. The units will still be mL.
- In the space for Equation, use the Variables drop-down menu to choose "Volume". Do not type this in directly. Once it’s entered into the Equation space, simply type "+0.8". This has the effect of adding 0.8 mL to each of the values you have previously entered, but in a new column of the data table.
- By clicking
you get back to the graph. Move the cursor so it is over the "Volume" label on the x-axis. Press the left mouse button and note that you can select "Real Volume" from the menu that appears.
- Now do a new curve fit as in Step 9. Compare the results of this fit with the previous one. Have you accounted well for the extra volume?
Constant Factor
- One way to determine if a relationship is inverse or direct is to find a proportionality constant, k, from the data. If this relationship is direct, k = P/V. If it is inverse, k = P•V. Based on your analysis in steps 1-6, choose one of these formulas and calculate k for the seven ordered pairs in your data table (divide or multiply the P and V values).
- Under Data on the menu bar, choose New Calculated Column. Use a name like "Quotient" for P/V or "Product" for P•V.
- In the space for Equation, use the Variables drop-down menu to choose the variables, using either a forward slash "/" or asterisk "*" to represent division or multiplication. These new values will be entered into a new column of the data table.
- By clicking
you get back to the main page. Click on the Data Table and use the scroll bar at the bottom to move to your Quotient or Product column.
- How constant were the values you obtained in Step 12? Good data may show some minor variation, but the values k should be relatively constant.
- Using P, V, and k (the value that you obtained in Step 12), write an equation representing Boyle’s law. Write a verbal statement that correctly expresses Boyle’s law.
- What experimental factors do we assume are constant in this experiment?
EXTENSIONSAnother Test
To confirm the type of relationship that exists between pressure and volume, a graph of pressure versus the reciprocal of volume (1/volume or volume-1) may also be plotted. To do this using Logger Pro, it is necessary to create a new column of data, reciprocal of volume, based on your original volume data.
- Remove the Curve Fit box from the graph by clicking on its upper-left corner.
- Choose New Calculated Column from the Data menu.
- Enter "1/Volume" as the Name, "1/V" as the Short Name, and "1/mL" as the Unit. Enter the correct formula for the column (1/volume) into the Equation edit box. To do this, type in "1" and "/". Then select "Volume" from the Variables list. In the Equation edit box, you should now see displayed: 1/"Volume". Click
.
- Click on the horizontal-axis label, select "1/Volume" to be displayed on the horizontal axis. You may need to re-scale the graph to examine it more closely.
- If the graph closely resembles a straight line, you can test this by clicking the Linear Fit button. The best straight line that can statistically be drawn through your data points is now drawn on the graph.
- How well does the straight line match your data points? A measure of how well it matches is given by the regression value, r =. If r = 1.000, the data perfectly fits a straight line. The further from 1.000 the regression value, the further from a perfect straight line.
Assuming you now have a straight line, use the values from your curve fit to complete the mathematical equation shown here:
A Further TestIn this test, we will explore the size of the volume discrepancy in a systematic way using analysis tools built into Logger Pro. At the end, we will be able to determine how much added volume we should have included when we did the analysis described above.
- Under Data on the menu bar, choose "User Parameters". Click on "Add". Define the new parameter as "Extra", starting value 0.000, units mL, and the increment 0.1. Click
.
- Under Data on the menu bar, choose "New Calculated Column". Use a name like "Adjusted Volume" and a short name like Va. The units will still be mL.
- In the space for Equation, use the Variables drop-down menu to choose "Volume". Do not type this in directly. Type "+", then use the drop-down menu "Parameters" to choose "Extra". This has the effect of adding a parameter that has an initial value of 0.0 mL to each of the values you have previously entered, but in a new column of the data table. (The equation will read "Volume"+"Extra".)
- Click
to get back to the graph. Move the cursor so it is over the x-axis label. Press the left mouse button and select "Adjusted Volume" from the menu that appears.
- Under Insert on the menu bar, choose "Parameter Control". This inserts a box in which the value of "Extra" is shown, but within which you can change the value by clicking on the up- or down-arrows. Position this control to the side of the graph, possibly overlapping the data table.
- Do a new curve fit as in Step 9. Compare the results of this fit with the previous one. We have not accounted for the extra volume, yet. The value of RMSE (Root Mean Square Error) may be relatively large.
- Now click the up-arrow in the Parameter Control box, adding 0.1 mL to each of the volume values. How does the RMSE value change? Making it smaller means the curve fit is better.
- Continue adding more volume until the RMSE value stops decreasing and begins to increase. Go back to the place where you obtained the smallest value for RMSE.
- Press the left-arrow on your keyboard. This has the effect of reducing the size of the steps in your parameter. Use the up- and down-arrows to get to the smallest value for RMSE again.
- Repeat step (i) two times. When finished, what is the value of the additional volume you determined should be added to the syringe’s reading to account for the extra air? How would you re-write this as a mathematical relationship?
ANOTHER IDEA
Try this same lab with syringes of different sizes. By looking at the additional volume needed to recover the Boyle’s Law relationship, you can examine how much of the additional volume is due to the syringe and how much of it is due to the additional volume inside the Gas Pressure Sensor.
AND TWO MORE IDEAS
1. You can have students experimentally measure the internal volume of the interface using the fit equation y = k/(x+a) where "a" is an experimental parameter. It will be about 0.8 mL for the end-valve type or about 1.5 mL for the side-mount fitting with a short hose. I figured this out last semester when a student did the PV lab with a short length of vinyl tubing (with unknown volume) and we had to salvage his data afterward.
2. A nice group exploration can extend this lab:
a. Each person at the lab table table starts with a different volume set on their syringe: 8.0, 10.0, 12.0, and (if a 4th person) either 9.0 or 11.0 mL.b. When graphing the data, make sure you record the equation in the best-fit parameters.
c. As a group, try to come up with a connection between the initial syringe volume (including the correction for tube & sensor volume) and the parameters in the best-fit equation.
d. As a group, write up an explanation for your findings. You should use Excel to plot the group's data. Turn in one copy with all participants' names. If you cannot make time for the write-up, each person may turn in an individual answer at a 2-point penalty if it is a solo answer or a 1-point penalty if it is a 2-person answer.
Thank you to Dave Blackburn, Century College, White Bear Lake, MN for these two nice additions.
This version was adapted from the Boyle's Law lab in Chemistry with Vernier from Vernier Software & Technology. Feedback to the author is always appreciated, especially if it results in additional extensions or corrections.Click here for MS Word version: boyle-2.doc
Click here for pdf version: boyle-2.pdf
Note that this version calls for direct connection to a computer using an appropriate Vernier interface (LabPro, Go! Link, or LabQuest). The same data could be collected using a TI graphing calculator using either Datamate or Easy Data, then transfered to Logger Pro. Or the data could be collected with LabQuest in standalone mode and transferred to Logger Pro. Once the data is transferred to the computer, the analysis can proceed as described above.
C.Bakken
Updated May 2009