|
CAPACITOR CHARGE/DISCHARGE 2 - LQ
|
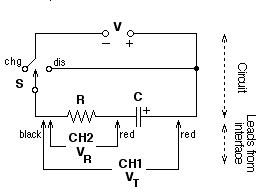
PURPOSEThe purpose of this lab is to examine the pattern of voltage vs. time and current vs. time for charging and discharging capacitors. In the process, you will examine the mathematical equation that describes the data.CIRCUIT

MATERIALS50-mF Capacitor, 47-KW Resistor, 1.5-volt cell, SPDT Switch, Wires, 2 Voltage Probes, Vernier LabQuest, LabQuest App., extra capacitors and resistors
CHARGING:
DISCHARGING:
ANALYSIS
DATA
|
Resistance, R |
|
|
||
|
Capacitance, C |
|
|
||
|
|
|
|
|
|
|
Exponent, C |
|
|
|
|
|
Product, RC |
|
|
|
|
|
Inverse RC, (RC)-1 |
|
|
|
|
|
% Difference |
|
|
|
|
MORE ANALYSIS
- If we examine the general equation for exponential decay, we could substitute the value Vo/2 for V(t), and solve for the time it takes for the voltage to drop to half its former value.
1/2 = e-t/RC
ln (1/2) = -t/RC
t1/2 = -RC ln (1/2) = 0.693 RC
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EXTENSIONS
CIRCUIT
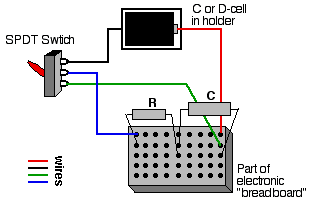
The following pictorial diagram shows one way that this lab can be carried out easily. The parts can be stored in a small space and can be used in part with other circuit labs. A DPDP switch could be substituted, or even a SPDT knife switch.
Click here to download this lab in an MS Word format - capacito2-LQ.docClick here to download this lab in a pdf format - capacito2-LQ.pdf
C. Bakken
November 2007