|
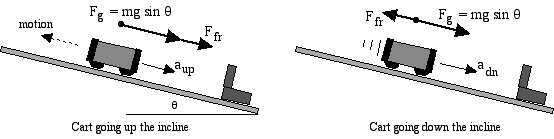
Theory:As a laboratory cart goes up or down an inclined plane, it will be under the influence of two primary forces - gravity and friction. While it is comforting to consider only gravity, to fully understand the data one collects with a Motion Detector, you need to include friction in your work.
As the cart moves uphill (below left), the component of gravity and the friction force are both acting against the motion. This results in acceleration that we will call aup. This is the acceleration that slows the cart while it is going uphill. From Newton's Second Law of Motion: Fnet = ma = (Fg + Ffr) = m aup .

As the cart moves downhill (above right), the component of gravity pulls it down while the friction force pulls uphill, working against its motion, resulting in adn. Using the Second Law: Fnet = ma = (Fg - Ffr) = m adn . Note that absolute values of acceleration have been used in these two equations.Purpose:
As you study the acceleration of a laboratory cart on an incline, you will use the motion of the cart to determine the angle of the incline and calculate the effective friction force acting on the cart.
Equipment:
Macintosh or PC Computer, Inclined Plane (ramp or dynamics track), Laboratory Cart, Meter Stick, Go! Motion or Motion Detector and LabPro.
Procedure:
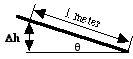 Set
up the inclined plane or dynamics track as shown above. Measure a
length of 1 meter along the incline starting at the point where it
touches the table. Measure the height from the table to the bottom
of the incline at this point, Dh.
Record this value in the Data Table. Measure and record the mass
of your cart, m. Limit Dh
to 5 cm maximum.
Set
up the inclined plane or dynamics track as shown above. Measure a
length of 1 meter along the incline starting at the point where it
touches the table. Measure the height from the table to the bottom
of the incline at this point, Dh.
Record this value in the Data Table. Measure and record the mass
of your cart, m. Limit Dh
to 5 cm maximum.Analysis:
Discussion Points:
Data Table:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Note to Teachers:Consider a performance-based assessment of this lab as follows: After allowing time to ask questions following the lab, hand the students a half-sheet of paper with two accelerations on it, one for going up the incline and one for going down. Ask them to tell you which one was the upward acceleration and which was the downward. Then have them tell you the angle of the incline. If they understood the lab well, they should be able to answer these two questions fairly quickly. And if they need to re-derive the equation, it isn’t too difficult.Consider this lab for a typical algebra-trig based college prep physics class. It can also be used effectively in an AP class.
Feel free to modify the items under Discussion to fit the needs of your students and your course as well as the time you wish to spend on this lab.
I believe this lab shows clearly why using technology can lead to deeper understanding of physical phenomena. We need to consider friction a real force that plays an ongoing part in our daily lives and we shouldn’t just eliminate or ignore it when studying physical situations.
Click here for MS Word version: Incline.doc
Click here for PDF version: Incline.pdfClick here for Word version for EasyData calculator: InclineEasy.doc
Click here for pdf version of the EasyData calculator: InclineEasy.pdfClick here for Word version for LabQuest: InclineLQ.doc
Click here for pdf version for LabQuest: InclineLQ.pdf
C. Bakken
Updated February 2008